这是我给出的结论,同学们还在最前面加上了审题这一重要步骤,既有效的完成了教学内容,又加深了同学们对这一知识点的认识,课堂气氛非常活跃。
然后就是实际问题的处理。我给出三道例题:“例1:某工厂生产甲,乙种产品,已知生产甲种产品lt需耗A种矿石lOt,B种矿石5t,煤4t,生产乙种产品1t需耗A种矿石4t,B种矿石4t,煤9t.每lt甲种产品的利润是600元,每1t乙种产品的利润是1000元.工厂在生产这两种产品的计划中要求消耗A种矿石不超过300t,B种矿石不超过200t,煤不超过360t.甲,乙这两种产品应各生产多少(精确到0.1t),能使利润总额达到最大?例2.咖啡馆配制两种饮料.每杯甲种饮料分别用奶粉,咖啡,糖9g,4g,3g;每杯乙种饮料分别用奶粉,咖啡,糖4g,5g,lOg.已知每天原料的使用限额为奶粉3600g,咖啡2000g,糖3000g.如果甲种饮料每杯能获利0.7元,乙种饮料每杯能获利1.2元,每天在原料的使用限额内饮料能全部售出,每天应配制两种饮料各多少杯能获利最大?”
这两道问题就是前面知识点的应用,我采取的是学生们在练习本上计算,然后把他们的笔记通过投影仪在大屏幕上展示,通过对比让他们认识到合理,规范的解题过程的重要性。
例3又是一道值得注意的问题:“某工厂有一批长为2.5米的钢管,要截成60厘米和42厘米两种规格的钢管,找出最佳下料方案。”很多同学不能找到合适的解决方案,经过讨论,我给出几何解释:
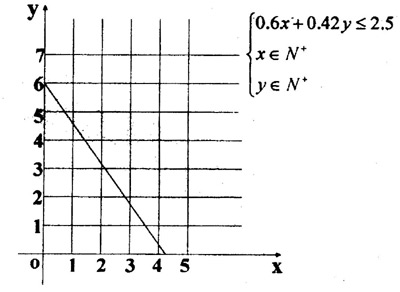
答案是x=2,y=3时损耗最少,在课堂上同学们并没有找到最佳解决方案。最后我给出一个作业:到附近的工厂、企业、商店、学校等作调查研究,了解线性规划在实际中的应用;或提出能用线性规划知识提高生产效率的实际问题,并做出解答,写出实习报告、研究报告或小论文。然后小结本节课的知识要点:
上一页 [1] [2] [3] 下一页
| 




